Criptografia de chave simétrica
2018-09-12 00:00
Se engana quem pensa que a criptografia surgiu recentemente. Apesar de ter se modernizado muito com o advento dos computadores, essa ciência já existe há milhares de anos, visto que o sigilo de informações não é uma necessidade recente. Na Roma Antiga, o ditador Júlio César (personagem crucial na transição da República Romana para o Império Romano) utilizava cifras para se comunicar com outros militares e governantes. É daí que vem o nome da famosa Cifra de César.
Mas afinal, o que é criptografia?
- Conjunto de princípios e técnicas utilizados para garantir comunicação segura, ainda que na presença de possíveis atacantes
- Além de garantir sigilo da informação, através da criptografia também é possível garantir autenticidade, através de assinaturas digitais
- Então, informalmente podemos dizer que a criptografia é utilizada para contar segredos em lugares públicos, falar sobre assuntos sigilosos por meios não confiáveis
Os algoritmos criptográficos que veremos hoje são denominados simétricos. Isso significa que para encriptar e decriptar mensagens a partir deles, a mesma chave (denominada chave simétrica) é utilizada. Para deixar mais claro, vamos supor que Alice e Bob queiram trocar mensagens sigilosas em um canal inseguro, bem como é o caso da Internet.
Para isso, ambos podem utilizar um desses algoritmos criptográficos e encriptar as mensagens, antes de enviá-las. Porém, eles precisam combinar uma chave e guardá-la com muito sigilo. Como fazer isso utilizando a Internet? Um atacante (que chamaremos de Eve) pode interceptar a conexão e obter a chave, sendo capaz de decifrar qualquer mensagem enviada por um dos dois. Esse é um problema muito delicado, mas deixaremos para explicar em detalhes numa futura palestra/postagem sobre algoritmos criptográficos de chave assimétrica. Então, vamos supor que eles tenham se encontrado em um bar e combinado a chave pessoalmente, antes do início da troca de mensagens.
Antes de enviar uma mensagem M para Bob, Alice utiliza o algoritmo criptográfico E, passando como parâmetros a chave privada K e a mensagem M. Agora ela pode enviar a mensagem encriptada E(M, K) para Bob sem se preocupar (caso o algoritmo seja bom), porque Eve até pode interceptar a mensagem, mas ela estará ininteligível. Bob, em posse da mesma chave K que Alice, pode utilizar o algoritmo D que decripta a mensagem, passando como parâmetro a chave K e obtendo a mensagem M em claro.

Essa é a ideia principal dos algoritmos de chave simétrica. Agora, veremos alguns exemplos muito famosos da criptografia clássica (fase anterior ao advento e popularização dos computadores). Atualmente, esses algoritmos são mais utilizados para o estudo da criptografia, e não são seguros. Porém, é muito importante entender como eles funcionam e quais são suas falhas.
Cifra de César

Usamos ela em um dos desafios iniciais do decifre.me! Segue a resolução dos 3 primeiros desafios
A Cifra de César é um dos algoritmos criptográficos mais simples. É uma cifra de substituição em que cada letra é trocada por outra que está a um número fixo de posições de distância. A chave é simplesmente esse número. Por exemplo, se a chave for K=4, a letra A será substituída por E. Seguindo essa lógica, o texto enigma seria transformado em IRMKQE.
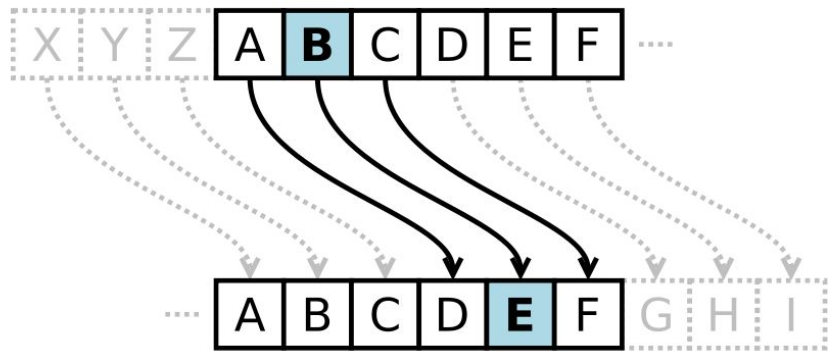
É fácil perceber que só existem 25 chaves para essa cifra, já que nosso alfabeto possui 26 letras. Logo, para quebrá-la, podemos executar o algoritmo com todas as opções de chave disponíveis até encontrarmos um texto que fique coerente.

Cifra de Substituição com Permutação do Alfabeto
Neste modelo, permutamos o alfabeto, gerando um alfabeto de substituição. Então, a letra a deve ser substituída por X, a letra x por J, e assim por diante. Há uma variação dessa técnica em que as letras também podem ser substituídas por símbolos não pertencentes ao alfabeto. Por exemplo, a por %, x por #, etc.
Por exemplo, podemos criar um alfabeto da seguinte forma:
| a | b | c | d | e | f | g | h | i | j | k | l | m |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | H | Q | G | I | U | M | E | A | Y | L | N | O |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F | D | X | J | K | R | C | V | S | T | Z | W | B |
Vamos pegar essa frase (acentos removidos propositalmente) como exemplo:
Os primeiros ativistas no final dos anos 1980, com o embrionario movimento dos Cypherpunks, ja atentavam para falta de seguranca em torno dos dados trocados na internet.
Cifrando com esse alfabeto, teríamos:
DR XKAOIAKDR PCASARCPR FD UAFPN GDR PFDR 1980, QDO D IOHKADFPKAD ODSAOIFCD GDR QWXEIKXVFLR, YP PCIFCPSPO XPKP UPNCP GI RIMVKPFQP IO CDKFD GDR GPGDR CKDQPGDR FP AFCIKFIC.
Quebrando a subsituição
E como atacamos isto? Dessa vez, temos muitas mais opções de chave do que na Cifra de César. Como cada variação do alfabeto é uma chave válida, temos 26! chaves! Isso é algo perto de 4 x 10^26. Logo, atacar esse problema com força bruta no número de chaves não parece uma boa alternativa. A fraqueza dessa cifra está em outro ponto. Mesmo se removêssemos espaços, números e pontuação, o texto ainda manteria uma estrutura muito próxima daquela existente no texto original, no que diz respeito ao histograma dos caracteres (a frequência em que eles ocorrem no texto). Quem percebeu isso foi um religioso árabe do século IX, enquanto tentava descobrir a data dos textos do Alcorão segundo a frequência de suas letras.
A Língua Portuguesa apresenta uma frequência média de ocorrência das letras nos textos. Essa frequência segue uma distribuição. Isso ocorre por causa da Lei de Zipf, que na verdade ocorre em todos os idiomas e não afeta somente a frequência das letras, mas também das palavras. Aliás, afeta muitas coisas além de linguística. Recomendo ver este vídeo se quiser saber mais.
Este é o histograma da língua portuguesa:
| Letra | Frequência |
|---|---|
| a | 15% |
| e | 13% |
| o | 11% |
| s | 8% |
| r | 7% |
| i | 6% |
| n | 5% |
| d | 5% |
| m | 5% |
| u | 5% |
| … | … |
Vamos tentar quebrar o seguinte texto (veja completo aqui):
ZG GAHLAL IVGU XGAZL IVG L WJMXBSHJLEML ZVJHMV JGWGABGUGABG. LXGZLJ NG BGJ
ZG USNGJAMKLNS UVMBS WSU S LNDGABS NSZ WSUXVBLNSJGZ, GZZL WMGAWML OL
GPMZBG YL UMRYLJGZ NG LASZ, DMZBS IVG S ZMHMRS NG MAESJULWSGZ ALS G
VUL AGWGZZMNLNG JGWGABG….
Se fizermos um histograma desse texto, obteremos a seguinte tabela:
| Letra | Frequência |
|---|---|
| L | 13.55% |
| G | 12.23% |
| S | 8.47% |
| Z | 8% |
| J | 7.81% |
| M | 7.81% |
| U | 5.83% |
| … | … |
Como é uma cifra de subsituição simples, a letra que foi substituída por L
era a letra que mais aparecia no texto original. Sabendo que o texto original
estava em português, existem muitas chances de L ser a letra a, G ser a
letra e e S ser o. Quanto maior o texto, mais isso é verdade, porque mais
se aproxima da frequência média. Em textos muito pequenos essa análise não irá
funcionar muito bem. As letras de menor ocorrência (x, k, w, y) serão
as que ficarão mais longe da posição correta, mas isso não é problema para nós,
já que as cinco primeiras letras já cobrem 50% do texto. A
relação entre o histograma do nosso texto e o da língua portuguesa não está
perfeita, mas substituindo corretamente apenas as cinco primeiras letras
obtemos (letras em maísculo ainda estão cifradas e minísculas estão em claro):
se eAHaAa IVeU XeAsa IVe a WrMXBoHraEMa sVrHMV reWeABeUeABe. aXesar Ne Ber se UoNerAMKaNo UVMBo WoU o aNDeABo Nos WoUXVBaNores, essa WMeAWMa Oa ePMsBe Ya UMRYares Ne aAos, DMsBo IVe o sMHMRo Ne MAEorUaWoes Aao e VUa AeWessMNaNe reWeABe.
Apareceu um essa, o que indica que estamos no caminho certo! Ainda não está
perfeito, mas algumas palavras estão chegando perto. Se repararmos nas palavras
quase completas, encontramos um trecho quase completo:
se eAHaAa IVeU XeAsa IVe a WrMXBoHraEMa sVrHMV reWeABeUeABe. aXesar Ne Ber se UoNerAMKaNo UVMBo WoU o aNDeABo Nos WoUXVBaNores, essa WMeAWMa Oa ePMsBe Ya UMRYares Ne aAos, DMsBo IVe o sMHMRo Ne MAEorUaWoes Aao e VUa AeWessMNaNe reWeABe.
aXesar Ne Ber se parece com “apesar de ser”, mas como o s já foi
resolvido pela letra Z, vamos supor que seja “apesar de ter”. Dessa forma,
resolvemos mais três letras:
X=pN=dB=t
Substituindo mais essas letras, o texto começa a ter forma:
se eAHaAa IVeU peAsa IVe a WrMptoHraEMa sVrHMV reWeAteUeAte. apesar de ter se UoderAMKado UVMto WoU o adDeAto dos WoUpVtadores, essa WMeAWMa Oa ePMste Ya UMRYares de aAos, DMsto IVe o sMHMRo de MAEorUaWoes Aao e VUa AeWessMdade reWeAte.
Vamos pegar outro trecho para analisarmos. Ya UMRYares de aAos se parece
muito com “há milhares de anos”. Dessa forma, encontramos Y, U, M, R e
A!
se enHana IVem pensa IVe a WriptoHraEia sVrHiV reWentemente. apesar de ter se moderniKado mVito Wom o adDento dos WompVtadores, essa WienWia Oa ePiste ha milhares de anos, Disto IVe o siHilo de inEormaWoes nao e Vma neWessidade reWente.
Estamos quase terminando, faltam poucas letras. Seguindo esse mesmo método, conseguimos terminar de decifrar o texto e sabemos qual a chave que foi utilizada, lembrando que a chave neste modelo é o alfabeto permutado. Por fim, temos o texto em claro:
Se engana quem pensa que a criptografia surgiu recentemente. Apesar de ter se modernizado muito com o advento dos computadores, essa ciência já existe há milhares de anos, visto que o sigilo de informações não é uma necessidade recente.
Cifra de Vigenère
Vamos supor que queiramos encriptar a frase reuniaodoenigmaquartafeira. É
escolhida uma chave qualquer, por exemplo, K=CARRO. Ela é então repetida até
atingir o tamanho da mensagem, gerando CARROCARROCARROCARROCARROC. Então, a
mensagem será encriptada assim: à primeira letra da mensagem (R) devem ser
adicionadas 2 unidades, pois a primeira letra da chave é C, terceira letra do
alfabeto. Então, o R é substituído por T. À segunda letra da mensagem (E),
0 unidades devem ser adicionadas, pois a segunda letra da chave é A. E assim
por diante. O resultado final é:
mensagem: reuniaodoenigmaquartafeira chave: CARROCARROCARROCARROCARROC cifra: TELEWCOUFSPIXDOSURIHCFVZFC
Qual a vantagem disso? Uma cifra feita desta maneira previne criptoanálise
sobre a frequência das letras, já que a letra que mais aparece nos textos em
português, a letra a, vai ser transformada em diversas letras: C, A, R e O.
Para facilitar nosso trabalho, usamos o “Quadrado de Vigenère”, que contem todas as rotações possíveis e as suas letras correspondentes.

Mas então, podemos utilizar a Cifra de Vigenère para encriptar mensagens? Na verdade, não. Ela também possui uma fraqueza, a natureza repetitiva da chave. Em 1863, Friedrich Kasiski foi o primeiro a publicar um ataque à Cifra de Vigenère. Ele se baseou no fato de que palavras repetidas de um texto podem acabar sendo cifradas pela mesma parte da chave. Por exemplo:
chave: ABCDABCDABCDABCDABCDABCDABCD texto: cryptoisshortforcryptography cifra: CSASTPKVSIQUTGQUCSASTPIUAQJBExemplo do [Wikipedia] (https://en.wikipedia.org/wiki/Vigen%C3%A8re_cipher)
A distância entre a repetição CSASTP é de 16 caracteres. Assim, todos os
divisores de 16 são possíveis tamanhos da chave K. Isso porque se o tamanho da
chave não fosse divisor de 16, a repetição não estaria a 16 caracteres
de distância da primeira ocorrência, já que na 16ª posição não teríamos o
primeiro elemento da chave. Então, por absurdo, ela só pode ter tamanho
1, 2, 4, 8, 16.
Caso o atacante perceba que há mais de uma repetição, ele pode utilizar o mesmo procedimento acima, obtendo outros conjuntos de divisores. Depois, basta calcular a intersecção entre esses conjuntos. Com isso ele sabe todos os possíveis tamanhos de chaves.
VHVSSPQUCEMRVBVBBBVHVSURQGIBDUGRNICJQUCERVUAXSSRTexto cifrado com Vigenère e mais de uma repetição visível
Utilizando algumas técnicas de estatística, como o teste de Friedman, é possível encontrar um tamanho de chave com maior probabilidade de ser o certo.
Após encontrado o tamanho da chave (no nosso caso, n=4), sabemos que ela é formada pelos caracteres K1 K2 K3 K4. Assim, a cada 4 letras do texto cifrado temos uma letra que foi cifrada pelo elemento K1 da chave. Com isso, podemos pegar só as letras que foram cifradas por K1 e fazer uma análise de frequência nelas, bem como fizemos nas Cifras de Substituição com Permutação do Alfabeto. Dessa maneira, podemos identificar quem é K1. O mesmo vale para os outros elementos da chave. Após identificar alguns valores da chave, começa a ficar mais fácil de decriptar o texto. Porém, esse método só é valido para textos relativamente grandes
DES (Data Encryption Standard) e AES (Advanced Encryption Standard)
São algoritmos criptograficos de chave simétrica da criptografia moderna. Ambos são baseados no operador exclusive or, o XOR (ou exclusivo).
0 XOR 0 = 00 XOR 1 = 11 XOR 0 = 11 XOR 1 = 0
Assim, suponha que você tenha uma chave K e uma mensagem M, ambas de mesmo tamanho. Se fizermos M XOR K, obteremos um resultado de mesmo tamanho:
mensagem: 0001010101010 chave: 1011101010100 cifra: 1010111111110
Note que é impossível recuperar a mensagem sem conhecer a chave
Porém, gerar chaves não determinísticas de mesmo tamanho que as mensagens é um processo muito custoso. O que é feito é utilizar chaves menores do que o tamanho da própria mensagem. Mas como já vimos na Cifra de Vigenère, repetir a chave não é uma boa ideia, pois um padrão pode ser formado na mensagem cifrada.
Por isso, o DES e o AES possuem métodos para expandir a chave sem gerar um padrão de repetição. Teremos então um dígito binário de chave para cada dígito binário da mensagem. Porém, o DES utiliza uma chave muito pequena (56-bits), facilitando um possível ataque.
- Em 1999, conseguiram quebrar uma mensagem encriptada pelo DES em aproximadamente 22h.
- Por esse motivo e outros (por exemplo, polêmicas sobre o envolvimento da NSA no design do algoritmo, influenciando a alteração do tamanho da chave do DES de 64-bits para 56-bits com o argumento de ser necessário utilizar os outros 8-bits como bits de paridade), o DES foi substituído.
- Tempo para quebrar uma mensagem encriptada pelo 256-bit AES: com um poder de processamento absurdo, de 50 supercomputadores capazes de checar 10^28 chaves por segundo (cada um deles), 3x10^51 anos seriam necessários para testar todas as possibilidades.
Decifre-me!
Mostre o que você aprendeu decifrando essas mensagens: https://enigma.ic.unicamp.br/talks/simetrico/desafio.txt
Referências
- The Code Book, por Simon Singh
- How secure is 256 bit security? [YouTube link] (https://www.youtube.com/watch?v=S9JGmA5_unY)