Criptografia de chave pública
criptografia chave assimétrica pública
2018-10-07 00:00
Há diversos algoritmos criptográficos de chave simétrica modernos e capazes de garantir comunicação confidencial em um meio inseguro. Dentre eles, o Advanced Encryption Standard (AES), por exemplo. Porém, esses algoritmos de chave simétrica exigem que os participantes da comunicação tenham em posse a mesma chave, denominada privada. Tratamos sobre esse assunto na palestra do dia 12/09/2018 e escrevemos um post sobre isso, caso queira dar uma lida!
O problema da distribuição de chaves
Mas então, como combinar chaves para realizar uma comunicação segura? Durante muito tempo isso foi feito pessoalmente. As pessoas se encontravam e combinavam uma chave, ou confiavam a um mensageiro essa tarefa. Outra alternativa era utilizar um canal seguro, já criptografado. Essas alternativas são custosas e pouco viáveis. Mas será que dá para fazer melhor?
Um pouco de história: Diffie-Hellman-Merkle

Na década de 70, a Internet começava a engatinhar, com o desenvolvimento da ARPANET pelos militares e cientistas das universidades norte-americanas. Atento ao cenário, o matemático Whitfield Diffie antecipava o advento da Internet como a conhecemos, com muitas pessoas utilizando computadores interconectados e trocando mensagens. Muitas delas confidenciais. Mas como a privacidade delas seria mantida? A troca de chaves privadas já era um problema, e isso se agravaria no futuro. Foi pensando nisso que Diffie começou a buscar desenfreadamente por uma solução.
Ao ouvir falar sobre Martin Hellman, que também estava muito interessado no problema, Diffie pegou seu carro e atravessou os Estados Unidos para que pudessem conversar. Diffie logo abandonou seu emprego e se inscreveu para entrar na graduação de Stanford e pesquisar com Hellman, que lecionava por lá.
Na mesma época, Merkle tentava se aprofundar no problema em um grupo de estudos do qual participava, também em Stanford. Porém, seu professor não viu muito futuro no tema, dizendo que não fazia sentido. Quando ficou sabendo sobre Diffie e Hellman, se aproximou dos dois e começou a fazer pesquisa com eles. Durante muito tempo buscaram por uma solução para o problema, o que criou bases para que, em 1975, Hellman a encontrasse.
A troca de chaves de Diffie-Hellman-Merkle
Em 1976, Martin Hellman e Whitfield Diffie (com contribuições de Ralph Merkle) publicaram o famoso artigo New Directions in Cryptography. Nesse artigo, uma maneira muito interessante de combinar chaves públicas em um canal de comunicação inseguro é proposto. Além disso, também apresentaram o conceito de chave pública, apesar de não terem encontrado um bom algoritmo para isso.
Em 1997, foi revelado que a agência de inteligência britânica já havia desenvolvido um esquema para a combinação de chaves em meios inseguros. Porém, isso foi mantido em segredo durante todo esse tempo. Há algumas teorias de que um dos militares vazou essas informações para Hellman, mas não há provas. Agora chega de blablabla e vamos entender como isso é possível.
Uma explicação simplificada
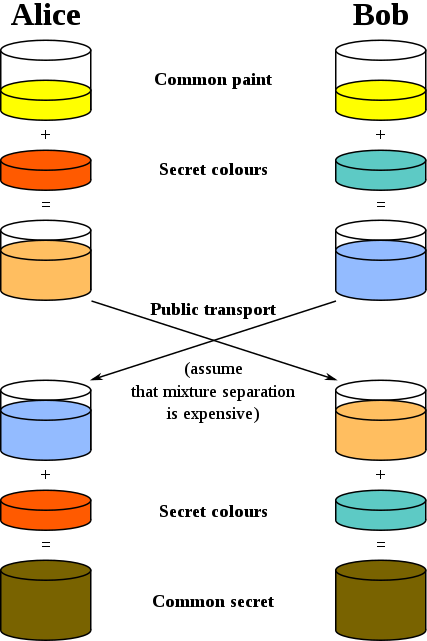
Para facilitar a compreensão do algoritmo de troca de chaves de Diffie-Hellman-Merkle, podemos utilizar cores. Vamos supor que Alice e Bob queiram combinar uma chave criptográfica, mas Eve esteja realizando um ataque na conexão insegura que eles utilizam. Então, Alice e Bob combinam uma cor pública qualquer, ou seja, uma informação que Eve também pode descobrir: amarelo. Agora, cada um escolhe uma cor secreta. Alice escolhe laranja e Bob escolhe azul. Depois, eles misturam a cor secreta com o amarelo. Alice obtém um balde de tinta laranja claro e Bob azul claro. Então, eles trocam essas misturas através do meio inseguro. Finalmente, basta eles misturarem a cor secreta que possuem com a mistura que receberam. E pronto, eles conseguiram uma cor secreta, que só eles dois conhecem. Essa seria a chave privada que eles obtiveram, ainda que utilizando uma conexão insegura.
Segue um vídeo com uma demonstração do algoritmo utilizando tintas.
Mas e se Eve, atacante do canal inseguro, conseguisse interceptar os baldes com: amarelo, azul claro e laranja claro? Não adiantaria, pois se misturasse tudo, teríamos: 2x amarelo, 1x azul e 1x laranja. O segredo é composto por: 1x amarelo, 1x azul e 1x laranja. A única forma de obter o segredo é pegar o balde com azul claro e tentar separar a cor pública, amarelo, da cor privada, azul. E depois fazer o mesmo para o balde com laranja claro: tentar separar o amarelo do laranja. Agora veremos um pouco de aritmética modular para que, matematicamente, verificarmos que é muito difícil “separar a cor pública da cor privada”.
Aritmética modular
Apesar do nome chique, aritmética modular é uma parte da matemática que temos muita intimidade; de fato, usamos ela todo dia! De maneira simples, operações modulares são aquelas onde “voltamos para o começo” depois de um certo número ser atingido - ou seja, depois de toda conta, dividimos o resultado por um certo número e ficamos apenas com o resto dele.
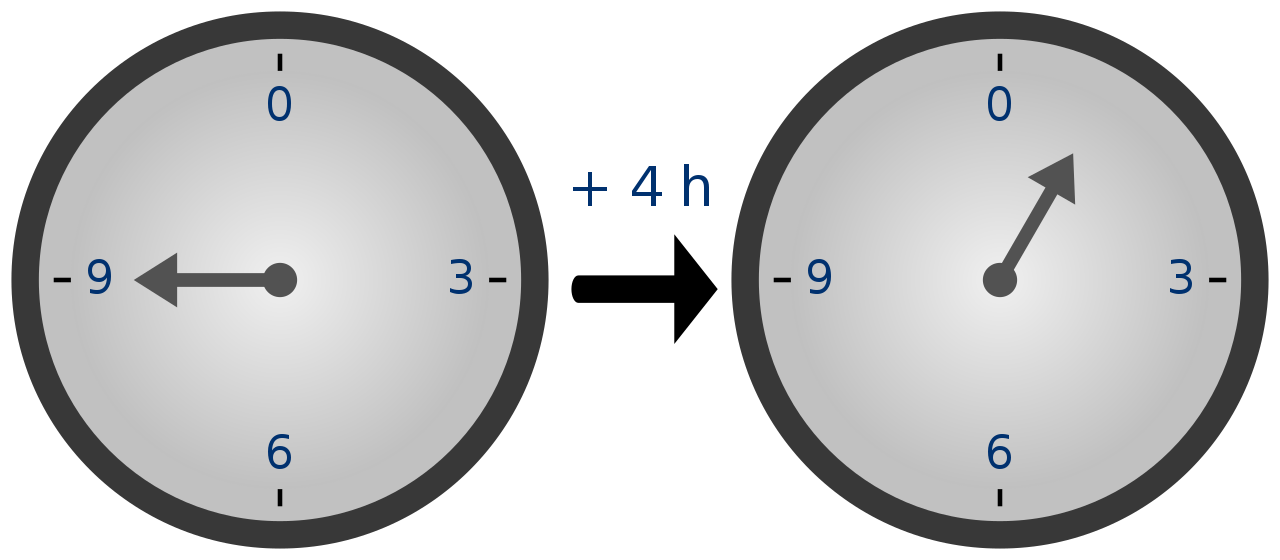
Conseguiu imaginar algo cotidiano que funciona assim? Nós fazemos essas contas
todo dia ao olhar para o relógio. Pense: Se são 9h da manhã e você tem um
compromisso dali a quatro horas, como você descobre que horas é o compromisso
num relógio (analógico)? Primeiro fazemos 9+4 = 13, mas o relógio só conta
até 12 horas. Por isso, ao passar de 12h, voltamos para o começo e começamos a
andar novamente no relógio. Como já gastamos 3 horas chegando de 9h até 12h, nos
falta contar apenas mais 1h; portanto, o compromisso é à 1h da tarde.
Podemos pensar nisso usando divisão, como citamos acima: Fazemos 9+4 = 13, e
então dividimos o resultado por 12. Como 13 = 12.1 + 1, o resto da divisão
de 13 por 12 é 1 - que é exatamente o número que procuramos! Geralmente
representamos essa operação de dividir e pegar o resto como módulo (daí o
nome aritmética modular), e escrevemos essa relação como13 (mod 12) ≡ 1 (mod 12). Note que não usamos o símbolo de = nesse caso, porque não
são de fato iguais, apenas quando fazemos esse módulo específico; ou seja, são
congruentes módulo 12. Se o número fosse 7, 13 (mod 7) ≡ 6 (mod 7),
então é importante ressaltar a diferença!
Podemos fazer diversas operações que conhecemos com módulo: adição, subtração, multiplicação, exponenciação, até mesmo fazer polinômios! Só precisamos tomar cuidado com coisas como divisão e raíz, porque essas só podem ser feitas em alguns casos específicos.
Uma última coisa interessante de se notar antes de passarmos para a matemática do algoritmo de Diffie-Hellman-Merkle é o que acontece com os números quando começamos a fazer exponenciação modular. Vamos começar elevando o 2 a diferentes potências no nosso relógio:
21 (mod 12) = 2 (mod 12) ≡ 2 (mod 12)
22 (mod 12) = 4 (mod 12) ≡ 4 (mod 12)
23 (mod 12) = 8 (mod 12) ≡ 8 (mod 12)
24 (mod 12) = 16 (mod 12) ≡ 4 (mod 12)
25 (mod 12) = 32 (mod 12) ≡ 8 (mod 12)
26 (mod 12) = 64 (mod 12) ≡ 4 (mod 12)
…
Chega um momento onde começamos a obter sempre os mesmos números. Isso é de
certa forma esperado - oras, se estamos falando de um número finito de
resultados possíveis (mais especificamente, no caso de mod n de 1 a n-1),
então é claro que em algum momento vamos repetir números. Mas apesar de no nosso
relógio termos 12 possibilidades, a partir da potência 3, ficamos repetindo
entre apenas 2 números, 4 e 8. Agora, um fato interessante: Se nosso número n,
no qual fazemos essas operações de módulo, for primo, temos certeza de que
haverão alguns números (o número exato, para os interessados, sendo o resultado
da função phi de Euler para n-1) que passarão por
todos os números de 1 até n-1, numa ordem aparentemente aleatória. E coisas
“aparentemente aleatórias” são muito, muito boas pra gente usar na criptografia.
Como um último exemplo, faça as potências de 2 agora usando mod 13. A
sequência dos 13 primeiros números agora fica da seguinte forma:
{2, 4, 8, 3, 6, 12, 11, 9, 5, 10, 7, 1, 2}
Demos uma volta completa passando por todos números entre 1 e 12! E mais do que isso, se alguém te perguntasse “Qual potência de 2 resulta em 10, módulo 13?”, você teria poucas opções para responder isso senão ir fazendo as contas na mão até chegar lá. Isso é conhecido como problema do logaritmo discreto, um problema reconhecidamente difícil de se resolver mesmo pelos nossos computadores atuais, e ele é utilizado não só no algoritmo a seguir como também no RSA, sobre o qual falaremos mais pra frente.
Voltando… algoritmo de Diffie-Hellman-Merkle matematicamente
Basicamente, o que acontece é que uma função difícil de calcular sua inversa
deve ser encontrada. Ou seja, uma função f tal que, dado um x,
calcular f(x) = y é fácil. Mas dado um y, é muito difícil
encontrar x de uma maneira eficiente. Então, eles tiveram a seguinte ideia:
- Alice escolhe 2 números g e p (com algumas características especiais) e os envia para Bob.
- Alice escolhe um valor secreto a tal que 1 <= a < p, calculaA = ga mod p e envia o resultado para Bob.
- Da mesma forma, Bob escolhe um valor secreto b tal que1 <= b < p, calcula B = gb mod p e o envia para Alice.
- Agora, Alice calcula Ba mod p e Bob calcula Ab mod p.
Talvez não pareça, mas Ba mod p ≡ Ab mod p. Observe:
Ba mod p ≡ Ab mod p (gb mod p)a mod p ≡ (ga mod p)b mod p (gba mod p) ≡ (gab mod p)
Isso é MUITO legal. Alice e Bob chegaram em um mesmo valor sem que tenham enviado o valor secreto de um para o outro. Mas como garantimos que isso é seguro de um possível atacante?
Tentativa de ataque
Vamos supor que Eve esteja atacando a conexão insegura de Alice e Bob e tenha obtido p e q. Além disso, Eve obtém A e B, ambos transmitidos pela rede. Para obter o valor que Alice e Bob calcularam no acordo (ou seja, a chave criptográfica), a e b são necessários. A única forma de obtê-los é a partir de A = ga mod p e B = gb mod p. Se não fosse o mod na fórmula, bastaria aplicar log em ambos os lados da equação. Mas, como já vimos, o mod atrapalha tudo.
Segue um vídeo com uma explicação do porque é difícil calcular o logaritmo com o mod na fórmula.
Mas há uma outra forma de explorar vulnerabilidades no algoritmo. Um ataque de man-in-the-middle é factível. Eve pode se passar por Bob, e combinar uma chave A com Alice, e depois, se passar por Alice e combinar uma chave B com Bob. Assim, quando Bob for enviar uma mensagem para Alice, na verdade vai enviar para Eve, que vai decriptar com a chave B. Depois, Eve encripta a mensagem com a chave A e envia para Alice.
Outro problema do algoritmo
Já falamos sobre uma maneira de combinar chaves simétricas em um meio inseguro. Mas por que Diffie, Hellman e Merkle não pararam por aí? Porque o algoritmo deles não é perfeito. Há algumas limitações. Por exemplo, vamos supor que Alice nunca tenha entrado em contato com Bob, e eles vivem em regiões que possuem fusos-horários distoantes. Enquanto Alice está acordada, Bob está dormindo, e vice-versa. Assim, se Alice for enviar um e-mail para Bob, ela precisará enviar uma mensagem para Bob, querendo combinar uma chave. Depois que Bob acordar, ele realizará sua parte do acordo, enviando uma mensagem para Alice. Finalmente, quando Alice acordar ela terá a chave privada, podendo enviar o e-mail em segurança para Bob.
Chave pública
Como já dissemos, Diffie, Hellman e Merkle também propuseram o conceito por trás dos algoritmos criptográficos assimétricos, ou seja, dos algoritmos de chave pública. Vamos entender qual é a ideia.
Nesses algoritmos, temos pares de chaves. Uma chave pública E, utilizada para encriptar as mensagens, e outra chave privada D, para decriptar as mensagens encriptadas com E. Apesar de relacionadas, é impraticável atacar E para obter D. Assim, o detentor de um par de chaves pode disponibilizar a chave pública para todos. Qualquer mensagem encriptada com essa chave só pode ser decriptada por ele, que possui a chave privada correspondente. O primeiro desses algoritmos - o RSA - foi proposto por Ron Rivest, Adi Shamir, e Len Adleman, um ano após a publicação do famoso artigo de Diffie e Hellman.
RSA
Apesar de ser muito famoso e ser utilizado até hoje, a ideia central do RSA é bem mais simples do que é de se esperar. É claro, no mundo real temos várias outras coisas para se levar em conta então as coisas ficam bem mais complexas, mas a essência do RSA é a seguinte:
Geração de chaves
- Gere dois números primos distintos, aleatórios e grandes,
peq - Calcule N = p.q
- Calcule Φ = (p-1).(q-1)
- Escolha um número
e, 1 < e < Φ, tal que mdc(e,Φ) = 1. - A operação passada garante que existe um número único
dtal que e .d ≡ 1 (mod Φ), então calculamos ele.
Temos assim um par de números que é nossa chave pública (e, N) e um número
que é nossa chave privada (d). Não vamos entrar em muitos detalhes aqui,
mas saiba que os números e e d, escolhidos dessa forma, garantem que
para qualquer x entre 1 e N-1,
xed mod N ≡ x mod N.
Ainda parece estranho, não é mesmo? Sabendo de tudo isso, vamos para os
algoritmos de encriptação e decriptação em si, que vão fazer as coisas fazerem
muito mais sentido.
Encriptação com o RSA
- Obtenha a chave pública do seu destinatário
(e, N) - Represente sua mensagem
mcomo um inteiro entre 1 e N-1. (PS: podemos olhar os bits de uma mensagem como um numerão, por exemplo!) - Calcule c = me mod N
E é isso! c é agora sua mensagem cifrada, e alguém que queira descobrir
sua mensagem teria que saber que raio de número m elevado a e resulta
em c quando isso é feito mod N; e como vimos, isso é uma coisa muito
complicada de se resolver. Vamos agora para a decriptação:
Decriptação com o RSA
- Utilize sua chave privada
dpara calcular m = cd mod N.
E acabou! …É sério, acabou mesmo. Falei que era simples! Do jeito que as
chaves foram escolhidas, como c = me mod N, então
m = cd mod N = med mod N ≡ m mod N, e como
a mensagem m está entre 1 e N-1, a operação de módulo não vai mudar nada
nela, e ela vai chegar intacta.
E apesar da simplicidade, é esse mesmo algoritmo - com algumas mudanças para evitar alguns outros tipos de ataque, como ataques de canal lateral - que é usado para quase tudo que usa criptografia de chave pública hoje em dia.
Esperamos que tenha gostado e se impressionado tanto quanto a gente, porque criptografia é um negócio muito legal!